Have you ever wondered why some numbers can be split evenly by other numbers? That’s where factors come in! In this guide, we will learn about the factors of 60. Understanding factors is very useful. It helps with simple math, like sharing candies, dividing toys, or even planning your time.
For example, if you have 60 candies and want to share them equally with your friends, knowing the factors of 60 makes it easy to see who gets how many. Factors are also important in school math. They help with problems in multiplication, division, and fractions.
The number 60 is interesting because it has many factors. This means it can be split in lots of ways. In math, we call numbers like this composite numbers. Learning arithmetic factors and integer factors helps you solve problems quickly.
By the end of this article, you will know all the factors of 60. You will see simple ways to remember them and use them in real life. You will also learn about prime numbers that make up 60 and how to make a factor tree. Let’s start this math adventure and see why 60 is such a special number!
What Are Factors?
A factor is a number that divides another number exactly. This means there is no remainder. For example, 2 is a factor of 6 because 6 ÷ 2 = 3. Another word for a factor is divisor.
Factors can be positive or negative. Positive factors are numbers like 1, 2, or 3. Negative factors are numbers like -1, -2, or -3. Both work in math, but we usually use positive numbers first because they are easier to see and count.
Let’s look at divisors of 60. These are the numbers that can divide 60 perfectly. Factors help us find common divisors, which are numbers that divide more than one number. For example, 2 divides both 6 and 60, so it is a common divisor.
We can also use integer division to check if a number is a factor. If 60 ÷ 5 = 12, then 5 is a factor. This is called factor analysis in math.
Here is a simple table to help you understand:
| Term | Simple Explanation | Example |
|---|---|---|
| Factor | Number that divides another exactly | 2 divides 6, so 2 is a factor of 6 |
| Divisor | Another word for factor | 3 is a divisor of 6 |
Factors are everywhere. From sharing toys to cooking recipes, they help us divide things fairly. Learning about factors makes math easier and more fun!

Complete List of Factors of 60
Now that we know what factors are, let’s list all the factors of 60. These are all the numbers that divide 60 perfectly.
The positive factors of 60 are:
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
The negative factors are the same numbers but with a minus sign:
-1, -2, -3, -4, -5, -6, -10, -12, -15, -20, -30, -60
To make it easier, we can look at factor pairs. A factor pair is two numbers that multiply to 60. Here is a simple table:
| Factor Pair | Product |
|---|---|
| 1 × 60 | 60 |
| 2 × 30 | 60 |
| 3 × 20 | 60 |
| 4 × 15 | 60 |
| 5 × 12 | 60 |
| 6 × 10 | 60 |
These pairs show how 60 can be split evenly. You can use them to solve problems, like sharing 60 candies with friends or arranging 60 chairs in rows.
Knowing the numbers that go into 60 and the numbers 60 can make helps you with math. You can add numbers, make fractions smaller, and solve puzzles more easily.
Here’s an easy way to see all the factors of 60 and their pairs at a glance:
Factors and Factor Pairs of 60
Factor Pairs
Now that we see all factor pairs clearly, let’s learn how to break 60 into prime numbers.
Prime Factorization of 60
Every number can be broken into prime numbers. This is called prime factorization. Prime numbers are numbers that have only two factors: 1 and themselves.
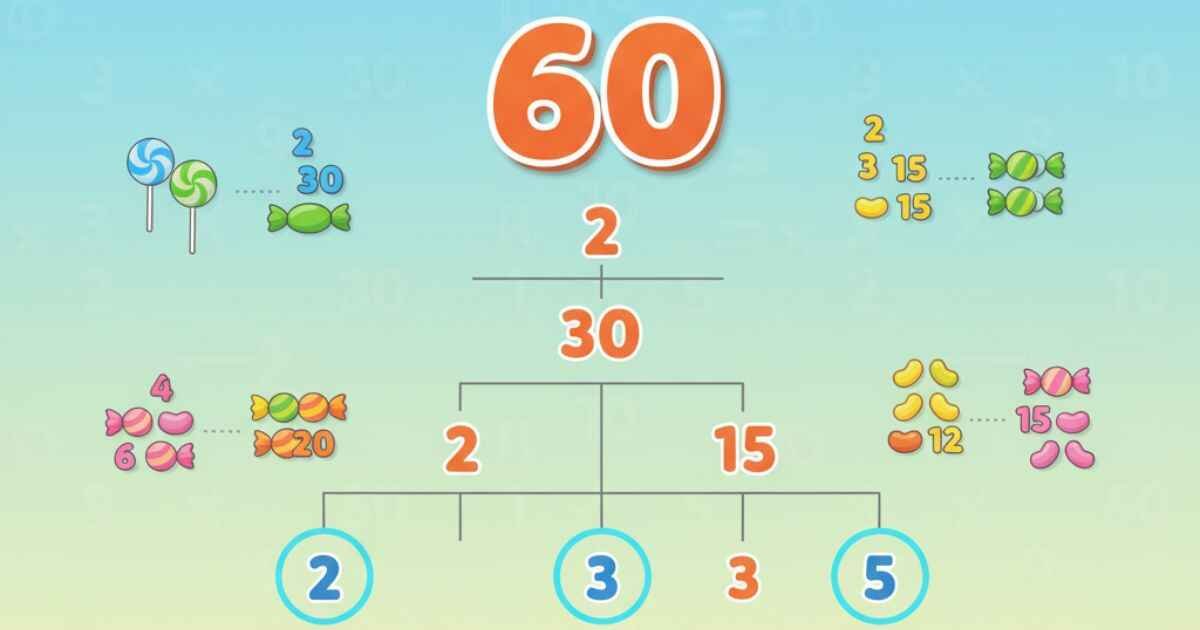
For 60, we can make a factor tree to see its prime factors:
| Step | Factor Split | Result |
|---|---|---|
| 60 | 2 × 30 | 2, 30 |
| 30 | 2 × 15 | 2, 15 |
| 15 | 3 × 5 | 3, 5 |
So, the prime factorization of 60 is:
60 = 2 × 2 × 3 × 5 or 2² × 3 × 5
Prime factorization is important because it helps us find greatest common divisors and least common multiples easily. It also makes division and multiplication faster.
Using prime numbers, you can check if a number divides 60. For example, 2, 3, and 5 all divide 60 because they are part of its prime factorization.
Learning the factorization process is like breaking a big puzzle into small pieces. It also teaches prime decomposition, which helps with fractions, ratios, and math games.
Lets Read Our Latest Post: YouTube Premium Plans Compared: Save or Overpay?
Understanding Factor Pairs
Factor pairs are a fun way to see how numbers work. A factor pair is two numbers that multiply to give another number.
For 60, some factor pairs are:
- 1 × 60
- 2 × 30
- 3 × 20
- 4 × 15
- 5 × 12
- 6 × 10
You can also use objects to understand factor pairs. Imagine you have 60 apples. You can make rows and columns:
- 2 rows of 30 apples
- 3 rows of 20 apples
- 6 rows of 10 apples
Factor pairs are symmetrical. This means if 2 × 30 = 60, then 30 × 2 = 60. Knowing this helps with arithmetic calculations and number decomposition.
Factor pairs also make division easy. If you know one factor, you can find the other by dividing 60 by it. This is integer division in action.
Divisibility Rules for 60
Divisibility rules help us quickly check if a number can divide 60 without doing long division.
Here are some easy rules:
| Divisor | Rule | Example |
|---|---|---|
| 2 | Number is even | 60 ÷ 2 = 30 |
| 3 | Sum of digits divisible by 3 | 6 + 0 = 6 → 6 ÷ 3 = 2 |
| 5 | Ends with 0 or 5 | 60 ÷ 5 = 12 |
| 6 | Number divisible by 2 and 3 | 60 ÷ 6 = 10 |
Using divisibility tests, you can check numbers fast. For example:
- 2, 3, 5, and 6 all divide 60 perfectly.
- Numbers like 7 or 8 do not divide 60 evenly.
Knowing factors and the rules for dividing numbers helps you with homework, playing math games, and counting things in real life.
Applications of Factors of 60
Factors of 60 are not just for school math. They are useful in daily life too!
One way to use factors is simplifying fractions. For example, if you have 30/60, you can divide both the top and bottom by 30. This makes the fraction 1/2.
Factors are also helpful in scheduling or dividing time. There are 60 minutes in an hour. You can split 60 minutes into 2, 3, 4, 5, or 6 parts. This helps plan activities, games, or study time.
In school or coding problems, knowing factors makes calculations faster. For example, if a teacher asks you to group 60 pencils equally, you can use factor pairs to find how many pencils go in each group.
Here are some example problems:
| Problem | Solution Using Factors |
|---|---|
| Share 60 candies equally among 5 friends | Each gets 12 |
| Reduce fraction 20/60 | 1/3 |
| Divide 60 minutes into 4 equal parts | Each part is 15 minutes |
Factors also help with greatest common divisors (GCD) and least common multiples (LCM). These are used in number theory and mathematical operations like adding fractions or solving word problems.
Knowing factors of 60 makes math easier and faster. You can split, group, and plan things quickly.
Also Read: Creating Lasting Memories from Everyday Journeys
Pros and Cons of Understanding Factors
Learning factors has many advantages:
- Simplifies math: You can divide and multiply numbers faster.
- Helps with GCD and LCM: This makes adding fractions and other problems easier.
- Easy fraction reduction: Fractions like 20/60 become simple to understand.
But there are some challenges too:
- Can be confusing at first: Beginners may forget some factors.
- Needs practice: You have to try many problems to get better.
The best way to learn is by practicing with small numbers first, like 12 or 24, and then try bigger numbers like 60. Doing exercises makes factor analysis easier and helps with arithmetic calculations in real life.
You May Like This Article: Explore Cave Springs Cowboy Camp: Hidden Utah Desert Treasure
Fun Facts About 60 and Its Factors
The number 60 is special! Here are some fun facts:
- There are 60 minutes in an hour.
- A circle has 360 degrees, which is a multiple of 60.
- 60 is a highly composite number, meaning it has many factors.
- Ancient cultures used 60 for counting and time because it divides easily by many numbers.
Knowing the factors of 60 can help you see patterns in numbers and even solve puzzles faster.
Common Questions About Factors of 60
Q1: What are all the factors of 60?
A: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 (also their negative numbers).
Q2: How do you find prime factors of 60?
A: Make a factor tree. 60 = 2 × 2 × 3 × 5.
Q3: Why is 60 considered highly composite?
A: Because it has many factors compared to smaller numbers.
Q4: How to quickly check if a number divides 60?
A: Use divisibility rules: check for 2, 3, 5, and 6.
Q5: How can I use factors in real life?
A: Sharing candies, splitting time, arranging chairs, or simplifying fractions.
Q6: What is the greatest common divisor (GCD)?
A: The biggest number that divides two numbers evenly. For 60 and 30, GCD = 30.
Q7: What is the least common multiple (LCM)?
A: The smallest number that both numbers fit into. For 60 and 15, LCM = 60.
Q8: Can factors help in math games?
A: Yes! You can group objects, solve puzzles, and plan moves easily.
Conclusion
Learning the factors of 60 is fun and useful. You can use them in school, games, and real life.
Knowing arithmetic factors, prime factorization, and factor pairs helps you divide things, simplify fractions, and solve problems faster.
Practice finding factors of 60 and other numbers every day. You will get better at integer division, factor analysis, and mathematical operations.
Remember, numbers like 60 are special because they have many ways to be split. Keep learning and using factors to make math easier and more fun!
Disclaimer
This article is for educational purposes only. The math examples and explanations are simplified for learning. Results may vary in different problems.

Shazny plays a key role behind the scenes, reviewing and refining content before it goes live. With a strong eye for detail, Shazny ensures that every article meets high standards of clarity, accuracy, and trustworthiness. From grammar checks to fact verification, Shazny helps maintain the quality and credibility of everything published on TryHardGuides.
Discover more from Try Hard Guides
Subscribe to get the latest posts sent to your email.